*Editor’s note: This article is the first in a three-part series. Plain text represents the writing of Greg Foss, while italicized copy represents the writing of Jason Sansone.
In February 2021, I published the first version of this article (find an executive summary here). While it received some very positive feedback, it also received lots of questions, particularly with respect to how bonds are priced. Accordingly, I wanted to update the research to include the most recent market data, as well as to clear up some of the more difficult concepts. I forget that math can be imposing for most people, yet since bonds and credit instruments are fiat contracts, bonds and credit instruments are pure math.
Over the last year, I have joined forces with an incredible team of like-minded Bitcoiners and together we endeavor to spread general knowledge about financial markets and Bitcoin. The team is named “The Looking Glass” and consists of people with diverse origins, ages and expertise. We are concerned citizens who want to help make a difference for the future, a future that we believe needs to incorporate a sound form of money. That money is bitcoin.
Immediately after I “met” Greg (listening to a podcast), I reached out to him on Twitter, and explained that, although I loved what he had to say, I only understood about 10% of it. I asked if he could suggest any supplemental educational material and he sent me a copy of his article, “Why Every Fixed Income Investor Needs To Consider Bitcoin As Portfolio Insurance.” Thank you, sir. I now think I understand even less…
Long story short, and after a few exchanges, Greg and I quickly became friends. Trust me when I tell you that he is as good and genuine of a human being as he seems. As he mentioned above, we quickly realized our shared vision and organized “The Looking Glass” team. Regardless, I still don’t understand most of what he says. I want to believe it’s all true, like when he states with conviction that, “Bitcoin is the best asymmetric trade I have seen in my 32 years of trading risk.”
But, as those of us in the Bitcoin community know, you need to do your own research.
Thus, the point is not whether you currently understand what he says, but rather, are you willing to do the work in order to understand? Don’t trust. Verify.
What follows is my attempt to verify and explain what Greg is saying. He has written the plain text content, while I have written the interposed italicized content in order to help translate his message for those of us who do not speak the same language. The rabbit hole is indeed deep… let’s dive in.
CREDIBILITY
This is my second attempt to link my experience in my 32-year career in the credit markets with the beauty of Bitcoin. Very simply, Bitcoin is the most important financial innovation and technology that I have seen in my career, a career which I believe qualifies me to have an informed opinion.
What I bring to the discussion is a vast experience in risk management and survival in the credit markets. I survived because I adapted. If I realized I had made a mistake, I exited a trade or even reversed a position. I believe my trading experience is somewhat unique in Canada. I think the various cycles I have lived through give me the wisdom to opine on why Bitcoin is such an important consideration for every fixed income and credit portfolio. The bottom line is: I never stop learning, and I hope the same for all of you… The world is dynamic.
Contrary to Greg, I have never “sat in a risk chair” or traded credit markets. But I do understand risk. I’m an orthopedic trauma surgeon. If you fall off of a roof or get crushed in a car wreck and shatter your femur, pelvis, forearm, etc., I’m the guy you meet. Does this make me an expert in credit, Bitcoin or trading? No. What I bring to the discussion is the ability to take complex situations, break them down to their foundational concepts, apply first-principle thinking and act with conviction. I thrive in chaotic environments where adapting in real time can mean life or death. The bottom line is: I never stop learning. The world is dynamic. Sound familiar?
CAREER HIGHLIGHTS
LATIN AMERICAN DEBT CRISIS
I worked at Royal Bank of Canada (RBC), Canada’s largest Bank, in 1988 when my job was to price C$900 million of Mexican debt for swap into Brady bonds. At this time, RBC was insolvent. So were all money center banks, hence the Brady Plan. The details aren’t necessarily important, but in short, RBC’s book value of equity was less than the write-down that would be required, on a mark-to-market basis, on its lesser-developed countries (LDC) loan book.
A brief explanation is required here: First, it is imperative to understand some basic concepts centered around “book value of equity.” What this refers to is the balance sheet of an entity (in this case, banks). In short, “balance” is achieved when assets equal liabilities and equity.
Think first about a house. Let’s say you purchased the home for $500,000. To do so, you made a $100,000 down payment and took out a loan from the bank for $400,000. Your balance sheet would appear as follows:
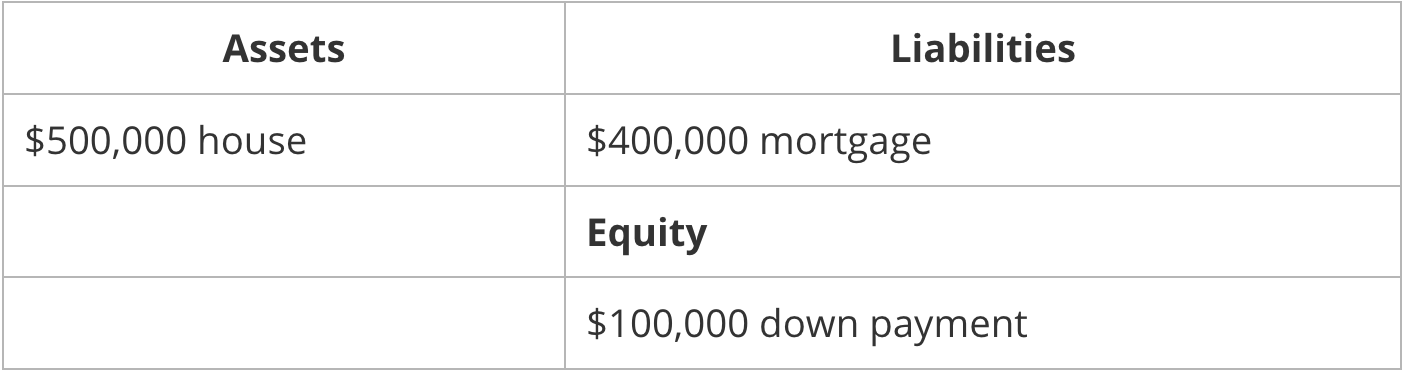
Let’s now say, for argument’s sake, your personal balance sheet is marked to market. This means that every day, your house is re-appraised at its market value. For example, on Monday it might be worth $507,030, on Tuesday $503,780, etc. You get the point. On Monday and Tuesday, in order to “balance,” your balance sheet reflects this appreciation in value (of your home) by accruing it to your equity. Good for you.
However, what happens if it is appraised at $496,840 on Wednesday? The balance sheet, now, has a problem, as your assets equal $496,840, while your liabilities plus equity equals $500,000. What do you do? You could balance the equation by depositing $3,160 into a bank account and holding it as cash. Phew, now your balance sheet balances, but you needed to come up with $3,160 in order to do so. This was, at best, an inconvenience. Luckily, in the real world, no one’s personal balance sheet is marked to market.
Let’s now go through the same exercise with a bank, specifically the Royal Bank of Canada in 1988 which, as Greg mentions, was levered 25 times relative to its book value of equity. In simplistic terms, its balance sheet would have looked something like this:
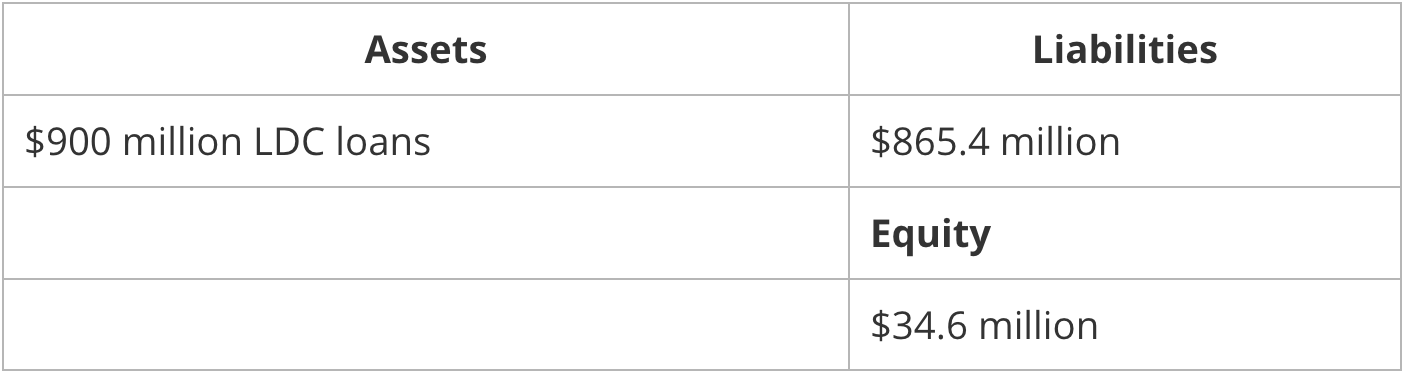
And unfortunately for banks, their balance sheets are marked to market — not on an accounting basis, but implicitly by “good” equity analysts. So, what happens if a string of defaults occurs within the pool of LDC loans, such that the bank will never see 1% of the $900 million owed to it? Perhaps this is a salvageable situation… just add $9 million to the assets as cash. But what if 10% of the $900 million loan book defaulted? What if the bank had to “restructure” nearly all of the $900 million loan book in order to recover any of it and it re-negotiated with the LDC clients to recapture only $600 million of the original $900 million? That’s an awful lot of cash to come up with in order to maintain “balance.”
Regardless, this was a scary discovery. Most, if not all, financial analysts on the equity desks had not done this simple calculation because they didn’t understand credit. They just felt, like most Canadians do, that the big six Canadian banks are too big to fail. There is an implicit Canadian government backstop. That is true, but how would the government backstop it? Print fiat dollars out of thin air. At that time, the solution was gold (since Bitcoin did not yet exist).
GREAT FINANCIAL CRISIS (GFC)
Note: This section may not make much sense now… we’ll break it all down in future sections. Fear not.
My experience with insolvent money center banks in 1988 would be re-experienced in 2008 to 2009 when LIBOR rates and other counterparty risk measures shot through the roof prior to equity markets smelling the rat. Again, in late 2007, equity markets rallied to new highs on Federal Reserve rate cuts while the short-term commercial paper markets were shut. The banks knew there was credit contagion looming and they stopped funding each other, a classic warning signal.
I worked at GMP Investment Management (GMPIM), a hedge fund, in 2008 to 2009 in the depths of the GFC. My partner was Michael Wekerle, who is one of the most colorful and experienced equity traders in Canada. He knows risk, and he quickly understood that there was no point in taking long positions in most equities until the credit markets behaved. We became a credit-focused fund, and bought up hundreds of millions of dollars of distressed Canadian debt in companies like Nova Chemicals, Teck, Nortel and TD Bank in the U.S. markets, and hedged by shorting the equity which traded mostly in Canada.
“Hedged by shorting the equity…” Huh? The concept of “hedging” is foreign to many retail investors and it deserves a brief explanation. Akin to “hedging your bets,” it involves effectively insuring yourself against a possible catastrophic outcome in the markets. Using the above example, “buying distressed debt” means you are purchasing the bonds of a company that may not be able to honor their debt obligations because you are able to acquire the right to that debt principal payout (at maturity) at a fraction of the cost. This is a great investment assuming the company doesn’t default. But what if it does? Your “hedge” is to sell the equity short. This short sale allows you to profit if the company were to enter bankruptcy. This is just one example of a hedging position. Other examples abound.
Nonetheless, this cross-border arbitrage was huge, and Canadian equity accounts had very little idea why their equity was relentlessly selling off. I remember one trade that was 100% risk free, and thus presented an infinite return on capital. It involved Nova Chemicals’ short-term debt, and put options. Again, the details aren’t important. Our CIO, Jason Marks (a Harvard University MBA graduate), believed in efficient markets and could not believe I had found a risk-free trade with huge absolute return potential. However, to his credit, when I showed him my trading blotter, and then asked “how much can I do?” (for risk limit considerations), his answer was beautiful: “Do infinity.” Indeed, there is tremendous value to adapting in a dynamic world.
At GMPIM, we also embarked on the defining trade of my career. It involved restructured asset-backed commercial paper (ABCP) notes. In short, we traded over C$10 billion of the notes, from a low price of 20 cents on the dollar, right up to full recovery value of 100 cents on the dollar. Asymmetric trades define careers, and ABCP was the best asymmetric trade versus risk I had seen up until that point in my career.
COVID-19 CRISIS
And then there was 2020… This time, the Fed did something totally new on the quantitative easing (QE) front: it started buying corporate credit. Do you think the Fed was buying corporate credit just to grease the lending runway? Absolutely not. It was buying because hugely-widening yield spreads (causing the value of credit assets to decrease, see balance sheet explanation above) would have meant banks were once again insolvent in 2020. Risky business, that banking… good thing there is a government backstop. Print, print, print… Solution: Bitcoin.
Quantitative easing (QE)? Most people don’t understand what the Federal Reserve (“Fed”) is actually doing behind the scenes, let alone what QE is. There is a tremendous amount of nuance here and there are very few people who actually understand this institution fully (I, for one, am not claiming to be an expert). Regardless, the Federal Reserve was originally established to solve inelasticity concerns around national bank currency. Through fits and starts, its role has changed dramatically over the years, and it now purports to act in accordance with its mandates, including:
- Target a stable inflation rate of 2%; and,
- Maintain full employment in the U.S. economy
If these sound nebulous, it’s because they are. Yet the argument could be made that the Fed now has effectively transformed into an entity that supports the debt-based global economy and prevents a deflationary collapse. How does it do this? Through many complex processes with high-brow names, but effectively, the Fed enters the open market and purchases assets in order to prevent a collapse of their value. This is called QE. And as you now know from the balance sheet discussion above, a collapse in the mark-to-market value of assets wreaks havoc on the financial system’s “plumbing.” How does the Fed afford to purchase these assets? It prints the money needed to buy them.
The GFC transferred excess leverage in the financial system onto the balance sheets of governments. Perhaps there was no choice, but there is no question that in the ensuing decade, we had the chance to pay down the debts that we had pulled forward. We did not do that. Deficit spending increased, QE was employed whenever there was a hint of financial uncertainty, and now, in my opinion, it is too late. It is pure mathematics.
Unfortunately, most people (and investors) are intimidated by math. They prefer to rely on subjective opinions and comforting assurances from politicians and central authorities that it is okay to print “money” out of thin air. I believe the credit markets will have a very different response to this indiscriminate printing, and this could happen in short order. We need to be prepared, and we need to understand why. “Slowly, then suddenly” is a reality in credit markets… Risk happens fast.
BACK TO (BOND) SCHOOL
As I mentioned above, asymmetric trades define careers. Bitcoin is the best asymmetric trade I have ever seen. Before I make such a large claim, though, I had better explain why.
I first attempted to do so one year ago, and you have provided me with questions and feedback so that Jason and I can refine the pitch. Together, we have crafted a document that I would be comfortable presenting to any fixed-income investor, large or small, to explain why bitcoin needs to be embraced as a kind of portfolio insurance.
Essentially, I argue that owning bitcoin does not increase portfolio risk, it reduces it. You are actually taking more risk by not owning bitcoin than you are if you have an allocation. It is imperative that all investors understand this, and we hope to lay out the arguments for why, using the credit markets as the most obvious class that needs to embrace the “money of the internet.”
But first, we need to be on a similar footing regarding our understanding of fixed income, and the various instruments that exist in the marketplace that allow for investors to take risk, manage risk (hedge), earn returns and/or experience losses.
Credit is really misunderstood by most small investors. In fact, in my opinion, credit is also misunderstood by many professional investors and asset allocators. As one of Canada’s first two sell-side high yield (HY) bond traders (the esteemed David Gluskin of Goldman Sachs Canada being the other), I have lived many head-scratching moments at the trading desks on Bay Street and Wall Street.
This summary is fairly general, and does not dive into the subtleties of various fixed income structures or investments. The purpose is to get everyone on a similar level so that we can propose a framework that will help future generations avoid the mistakes of the past. Indeed, those who don’t learn from history are doomed to repeat it.
Our plan is to start by explaining, in very general and simple terms, the credit markets with particular attention to bonds and bond math. From there, we will dive into bond risks and the typical mechanics of a credit crisis, and describe what is meant by “contagion” (in part two of this series). We will then conclude by presenting a valuation model for bitcoin when considering it as default insurance on a basket of sovereigns/fiats (in part three of the series).
(Note: This is a deep subject. For further reading, the Bible for fixed income investing is “The Handbook Of Fixed Income Securities” by Frank Fabozzi. This “handbook” is 1,400-plus pages of green eyeshade reading. It was required reading for my CFA, and it was usually visible, in multiple editions and stages of disrepair, on every trading desk where I have worked).
CREDIT MARKETS
To understand credit (and credit markets), one must first “zoom out” a bit to the broader financial asset market, which from a high level, can be illustrated as follows:
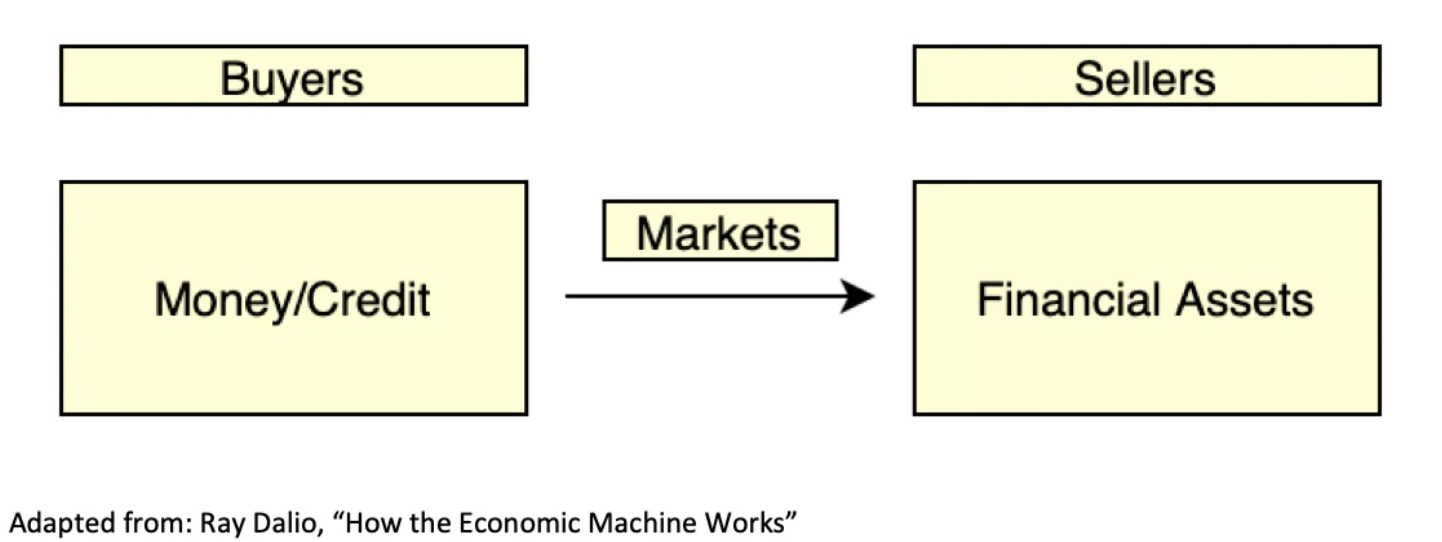
Illustrating the broader financial market.
The three main participants in this market are governments, corporations and individual investors. A glimpse at the breakdown of the U.S. fixed-income market demonstrates this:
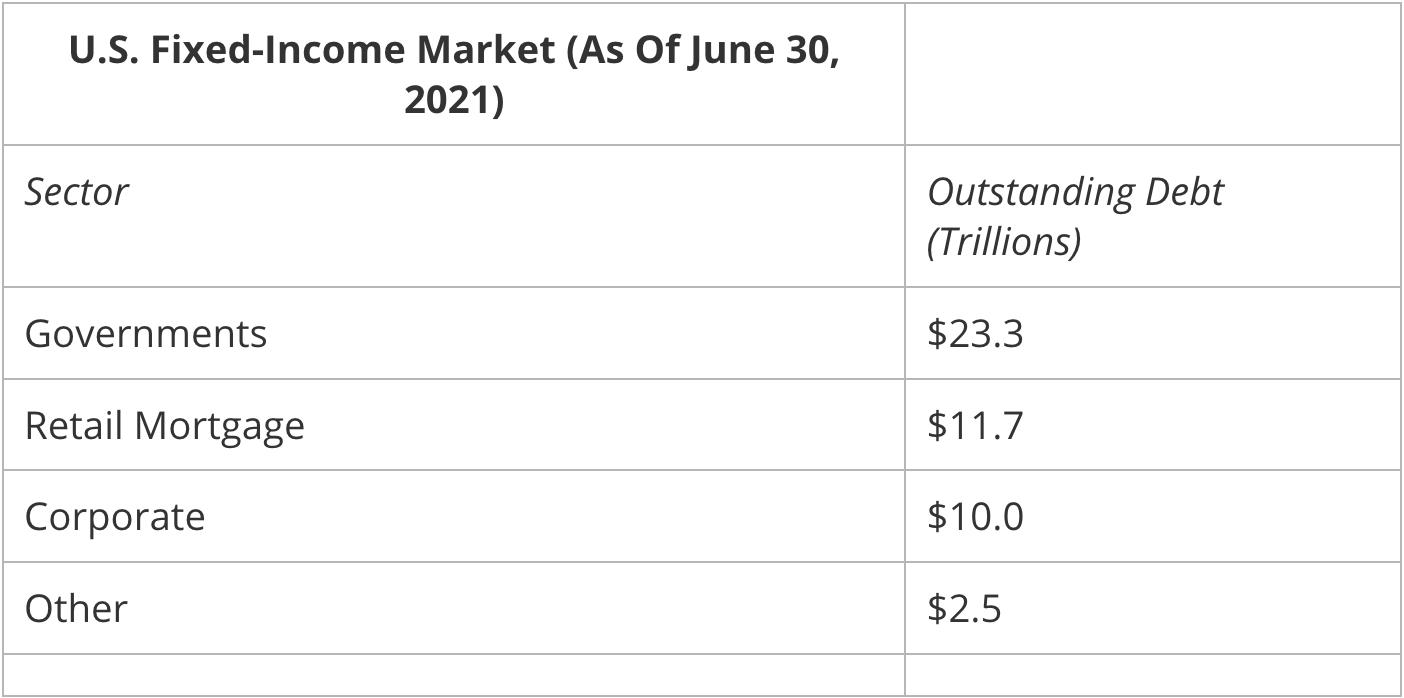
Data source: Securities Industry and Financial Markets Association (SIFMA)
So, why are financial assets bought and sold in the first place? Buyers of financial assets (investors) desire to stretch the present into the future, and forego the immediate availability of money/credit in the hope of generating yield/return over time. Conversely, sellers of financial assets (businesses, governments, etc.) desire to pull the future into the present, and access liquid capital (money) to serve present-day cash flow needs and develop future cash flow streams.
The following diagram highlights the “capital stack” (financial assets), that are available to buyers and sellers:
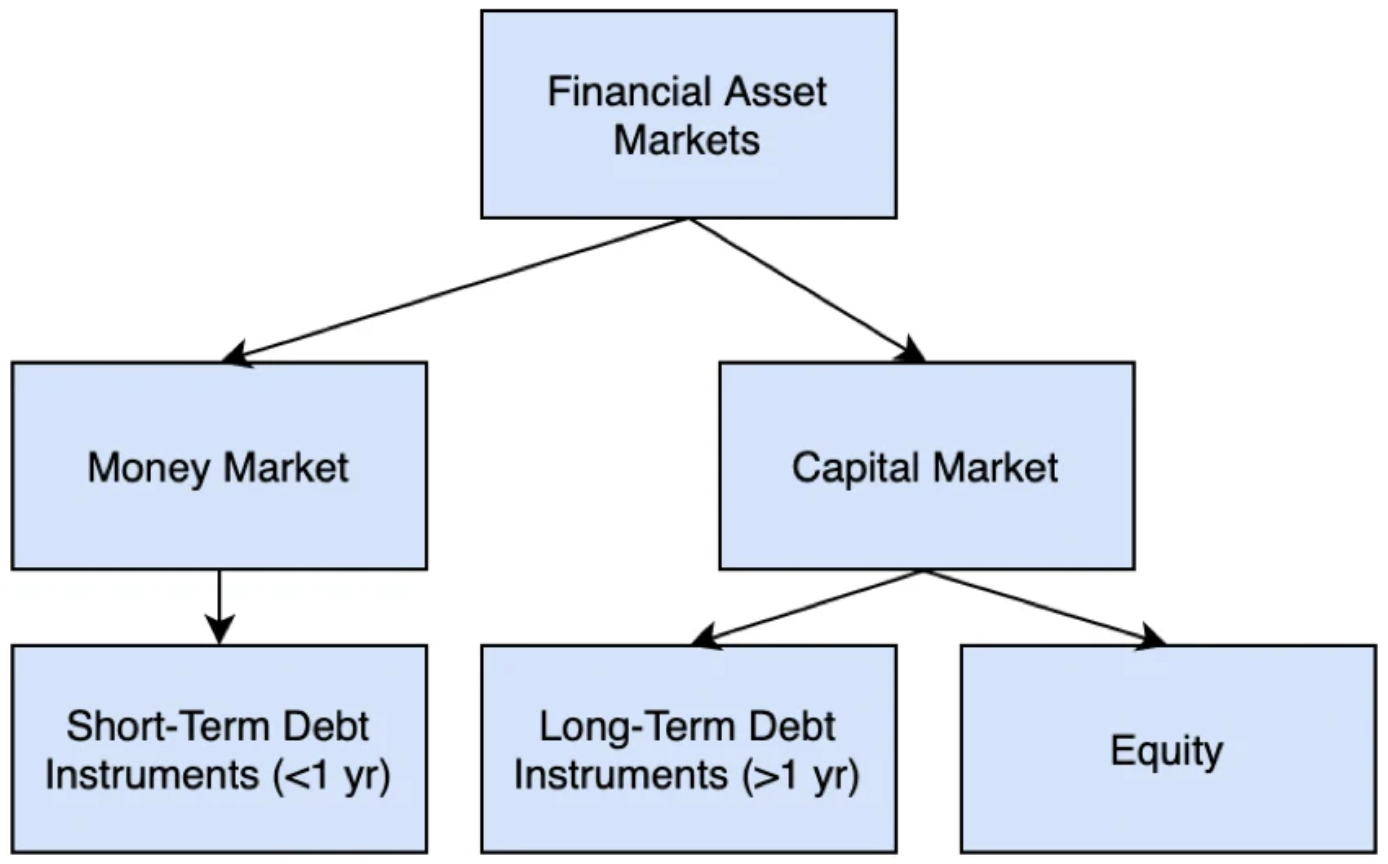
Capital stack available to buyers and sellers
There are many instruments within these markets, all of which accomplish similar goals for both the issuer and the purchaser. These instruments include, but are not limited to:
- Money market instruments, which are short-term debt agreements and include federal funds, U.S. Treasury bills, certificates of deposit, repurchase (“repo”) and reverse repo agreements and commercial paper/asset-backed commercial paper.
- Capital market debt instruments, which are long-term (more than one year) debt agreements and include: U.S. Treasury bonds, state/municipal bonds, “investment-grade” corporate bonds, “high-yield” corporate (“junk”) bonds and asset-backed securities (e.g., mortgage-backed securities).
- Equity instruments, which include common and preferred stock.
To put these markets into perspective, the size of the global credit/debt market is approximately $400 trillion according to Greg Foss and Jeff Booth, as compared to the global equity market, which is a mere $100 trillion.
Within this $400 trillion debt pool, the publicly-traded instruments (bonds) have varying terms to maturity, ranging from 30 days (treasury bills) up to 100 years. The name “notes” is applied to instruments maturing in two-to-five years, while “bonds” refer to 10-year terms, and “long bonds” refer to bonds with maturities of greater than 20 years. It is worth noting that terms of longer than 30 years are not common, although Austria has issued a 100-year bond. Smart state treasurer. Why? Because, as will be shown in subsequent sections, long-term funding at ultra-low rates locks in funding costs and moves the risk burden to the buyer.
INTEREST RATES AND YIELD CURVES
Pulling the future into the present and generating liquidity is not free. The buyer of the financial asset expects a return on their capital. But what should this return be? 1%? 5%? 10%? Well, it depends on two main variables: duration and risk.
To simplify this, let’s take risk out of the equation and focus strictly on duration. When doing so, one is able to construct a yield curve of U.S. treasuries as a function of time. For example, below is a chart taken from January 2021:

U.S. treasuries, January 2021
As you can see, the yield curve here is generally “upward-sloping,” implying that instruments of longer duration carry a higher yield. This is referred to as the “term structure of interest rates.”
We stated that the above takes risk “out of the equation.” If we accept the U.S. Treasury yield curve as the risk-free interest rate, we can calculate the appropriate rate on all other debt instruments from it. This is done by applying a “risk premium” above the risk-free rate. Note: this is also referred to as a “credit spread.”
Factors affecting the risk premium/credit spread include:

Factors affecting risk premium and credit spread
‘RISK-FREE’ RATES AND GOVERNMENT BORROWERS
Before diving deep into fixed income instruments/bonds, let’s first revisit this concept of the “risk-free rate” as it relates to government/sovereign borrowers…
Government bonds are the most widely held fixed income instrument: Every insurance company, pension fund and most large and small institutions own them. More specifically, U.S. government bonds have typically been called “risk-free” benchmarks, and thus the yield curve in the U.S. sets the “risk-free rate” for all given terms.
The shape of the yield curve is a subject of great economic analysis, and in an era when rates were not manipulated by central bank interference, the yield curve was useful in predicting recessions, inflation and growth cycles. Today, in an era of QE and yield curve control, I believe the predictive power of the yield curve is vastly diminished. It is still an extremely important graph of government rates, and the absolute cost of borrowing, but there is an elephant in the room… and that is the assertion that indeed these rates are “risk-free.”
To touch briefly on yield curve control (YCC)… Remember the discussion about the Fed supporting asset prices? YCC is when the Fed specifically supports treasury bond prices by not allowing the yield to increase above a certain threshold. Follow along in the coming sections, but hint: as bond prices fall, bond yields rise.
Given the reality of the exorbitantly-high debt levels contemporary governments have accrued, I do not believe you could claim there is no risk to the creditor. The risks may be low, but they are not zero. Regardless, we’ll get into the risk(s) inherent to fixed income instruments (specifically bonds) in subsequent sections. But first, some basics about bonds.
FIXED INCOME/BOND BASICS
As the name implies, a fixed-income instrument is a contractual obligation that agrees to pay a stream of fixed payments from borrower to lender. There is a payment obligation called “the coupon” in the case of a bond contract, or “the spread” in the case of a loan contract. There is also a term on the contract where the principal amount of the contract is completely repaid at maturity.
The coupon payment is defined in the debt contract, and is usually paid semi-annually.
Notably, not all bonds pay a coupon. Thus, there are two types of bonds:
- Zero-coupon/Discount: Only pay principal at maturity. The return for the investor simply involves “lending” an entity $98 to be paid $100 a year later (as an example).
- Coupon-bearing: Pay periodic coupon and principal at maturity.
For now, it is important to realize that lending is an asymmetric (to the downside) endeavor. If a borrower is doing well, the borrower does not increase the coupon or fixed payment on the obligation. That benefit accrues to the equity owners. In fact, if the risk profile has changed for the better, the borrower will likely pay down the obligation and refinance at a lower cost, which again benefits the equity. The lender can be out of luck since their more valuable contract is paid down, and they are not able to reap the attractive risk-adjusted returns.
To reiterate, the cash flows on a bond contract are fixed. This is important for a couple of reasons. First, if the risk profile of the borrower changes, the payment stream does not change to reflect the changed risk profile. In other words, if the borrower becomes more risky (due to poor financial performance) the payments are too low for the risk, and the value/price of the contract will fall. Conversely, if the risk profile has improved, the payment stream is still fixed, and the value of the contract will rise.
Finally, notice that we have yet to express our agreed upon unit of account in our “contract.” I imagine everyone just assumed the contract was priced in dollars or some other fiat denomination. There is no stipulation that the contract has to be priced in fiat; however, almost all fixed income contracts are. There are problems with this as will be discussed in future sections. For the time being, keep an open mind that the contracts could also be priced in units of gold (ounces), units of bitcoin (satoshis), or in any other unit that is divisible, verifiable and transferable.
The bottom line is this: The only variable that changes to reflect risk and market conditions is the price of the bond contract on the secondary market.
CREDIT VS. EQUITY MARKETS
It is my opinion that the credit markets are more ruthless than the equity markets. If you are right, you are paid a coupon and you get your principal returned. If you are wrong, the interest coupon is in jeopardy (due to the possibility of default), the price of the credit instrument starts to fall toward some sort of recovery value, and contagion comes into play. In short, I quickly learned to play probabilities and use expected value analysis. In other words: You can never be 100% certain of anything.
Given this, credit guys/bond investors (“bondies”) are pessimists. As a result, we tend to ask “how much can I lose”? Equity traders and investors, on the other hand, tend to be optimists. They believe trees grow to the moon, and are generally higher risk takers than bondies, everything else being equal. This is not surprising since their priority of claim ranks below that of credit.
In the event a corporate debt issuer is unable to make payment on a debt contract (default/bankruptcy), there are “priority of claim” rules. As such, secured debt holders have first right of claim to any residual liquidation value, unsecured debt holders are next to receive full or partial repayment of debt and equity holders are the last (usually receiving no residual value). Of note, it’s commonly understood that typical recovery rates of outstanding debt during a default are on the order of 35% to 40% of total liabilities.
Furthermore, if the common equity pays a dividend, this is not a fixed income instrument as there is no contract. The income trust market in Canada was built on this false premise. Equity analysts would calculate the “dividend yield” on the equity instrument and compare it to the yield to maturity (YTM) of a corporate bond and proclaim the relative value of the instrument. Too many investors in these income trusts were fooled by this narrative, not to mention the companies that were using valuable capital for dividend distributions instead of growth capital expenditures (“cap ex”). For the love of our kids, we cannot let this type of foolish money management ideology to fester.
If you manage money professionally, equities are for capital gains, whereas bonds are for capital preservation. Equity guys are expected to lose money on many positions provided their winners far outstrip the losers. Bondies have a more difficult balancing act: Since all bonds are capped to the upside, but their value can be cut in half an infinite number of times, you need many more performing positions to offset those that underperform or default. As such, bondies tend to be experts in risk. Smart equity investors take clues from the credit markets. Unfortunately, it is only a few who ever do.
BOND MATH 101
Every bond that trades in the secondary markets started its life as a new issue. It has a fixed contractual term, semi-annual coupon payment and principal value. Generally speaking, new issues are brought to market with a coupon equal to its YTM. As an example, a 4% YTM new issue bond is bought at a price of par (100 cents on the dollar) with a contractual obligation to pay two semi-annual coupons of 2% each.
After issuance, there is a fairly liquid secondary market that develops for the bond. Future bond trades are impacted by supply and demand due to such considerations as a change in the general level of interest rates, a change in the actual or perceived credit quality of the issuer or a change in overall market sentiment (risk appetite changes impacting all bond prices and implied bond spreads). A bond price is determined in an open market “over-the-counter” (OTC) transaction between a buyer and a seller.
The price of a bond is impacted by the YTM that is implied in the transaction. If the “market required yield” has increased due to credit risk or inflation expectations, the implied interest rate increase means that the price of the bond will trade lower. If the bond was issued at par, then new trades will occur at a discount to par. The opposite also applies.
For those of you who think the above makes good sense, feel free to skip this section. For the rest of us, let’s walk through bond math one step at a time.
We can value each type of bond, at issuance, in the following way:
Zero coupon/Discount: The present value of the future principal cash flow. The key component to this formula, and that which is often missed by beginners, is that the term “r” describes outside investment opportunities of equivalent risk. Thus:

Where:
- P = bond price today
- A = principal paid at maturity
- r = market required yield (current interest rate at which debt of equivalent risk is priced)
- t = number of periods (must match period of “r”) into the future the principal is to be repaid
Coupon-bearing: The sum of the present value of future cash flows from both coupon payments and principal. Again, the key component to this formula, and that which is often missed by beginners, is that the term “r” describes outside investment opportunities of equivalent risk. Thus:
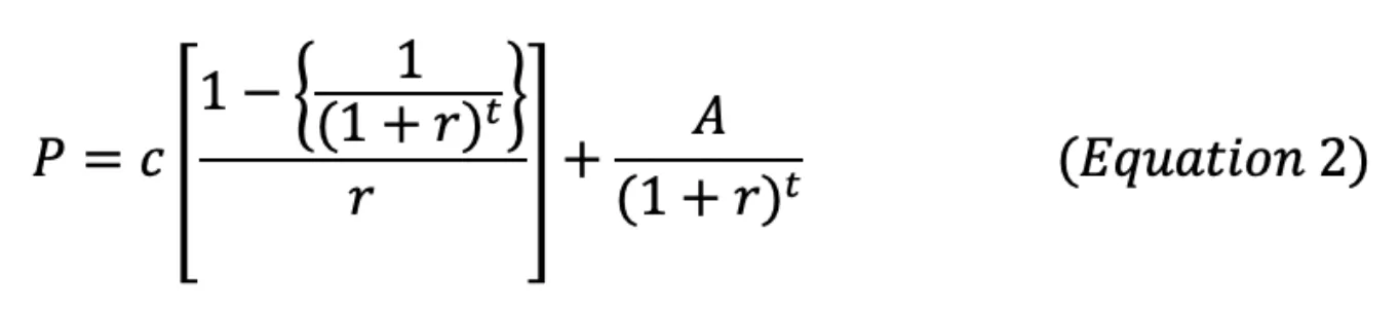
Where:
- P = bond price today
- c = coupon payment (in dollars)
- A = principal paid at maturity
- r = market required yield (current interest rate at which debt of equivalent risk is priced)
- t = number of periods (must match period of “r”) into the future the principal is to be repaid
Note: If the contractual coupon rate of a bond a is higher than the current rates offered by bonds of equivalent risk, the price of bond a increases (“premium bond”). Conversely, if the coupon rate of bond a is lower than bonds of equivalent risk, the price of bond a decreases.
Said differently, a bond’s price changes in order that its yield matches the yield of an outside investment opportunity of equivalent risk. This can also be illustrated as follows:
Note: “MY” is market required yield, “BY” is yield of bond that investor is holding.
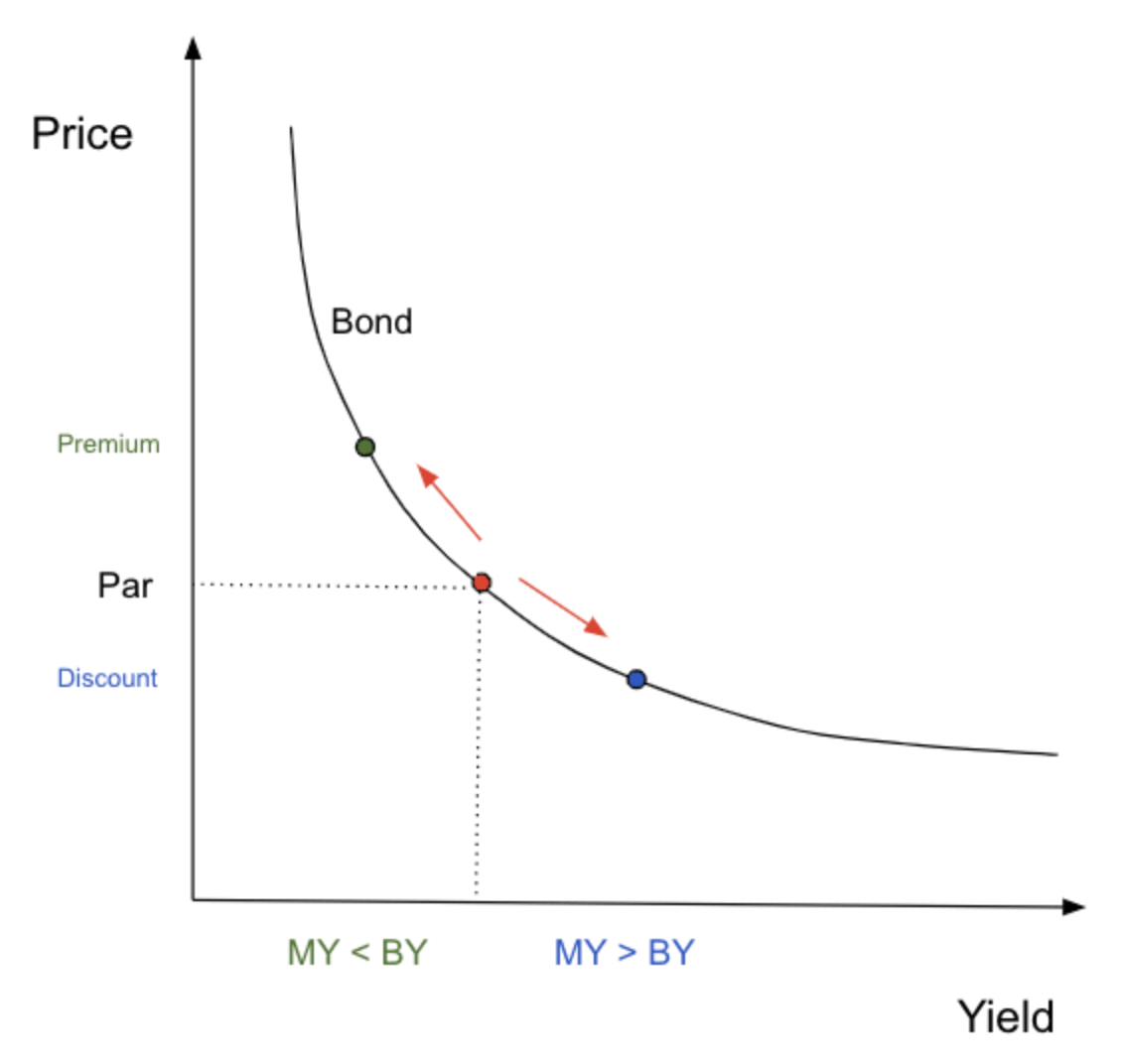
In considering the above equations and graph, the following truths become apparent:
- When a bond’s coupon rate is equal to the market yield, the bond is priced at par.
- When a bond’s coupon rate is less than the market yield, the bond’s price is less than par (discount).
- When a bond’s coupon rate is greater than the market yield, the bond’s price is greater than par (premium).
This is because bonds are a contract, promising to pay a fixed coupon. The only variable that can change is the price of the contract as it is traded on the secondary market. While we now understand how the prevailing interest rate in the market affects bond prices, it is important to note that this is not the only factor that can affect these prices. As we explored earlier, yields/interest rates reflect risk, and there is indeed more than one risk related to investing in a bond. We will explore these risks more in part two of this series.
BOND MATH 201
Calculating a change in bond price as a function of the change in “market required yield” using sensitivity analysis makes use of its first derivative (duration) and its second derivative (convexity) to determine a price change. For a given change in interest rate, the price change in the bond is calculated as negative duration times the change in interest rate plus one half of the convexity times the change in interest rate squared. If readers remember their physics formulas for distance, the change in price is like the change in distance, duration is like the velocity and convexity is like acceleration. It is a Taylor series. Math can be cool.
Math may, in fact, be cool, but it sure as hell isn’t fun sometimes. A couple of things to remember before we get deep into the mathematics:
- When the market required yield changes, the percent change in bond pricing is not the same for all bonds. That is, the following factors cause greater price sensitivity to a given change in market required yield: Longer maturity and lower coupon rate.
- The price increase of bonds (when market yields fall) is greater than the price decrease of bonds (when market yields rise).
DURATION: THE FIRST DERIVATIVE
So, then, what is the percent price change in a given bond for a given change in market-required yield? This is what duration gives us… strictly defined, duration is the approximate percentage change in a bond’s price for every 1% (100 basis points [bps]) change in market required yield. Mathematically, this is expressed as:
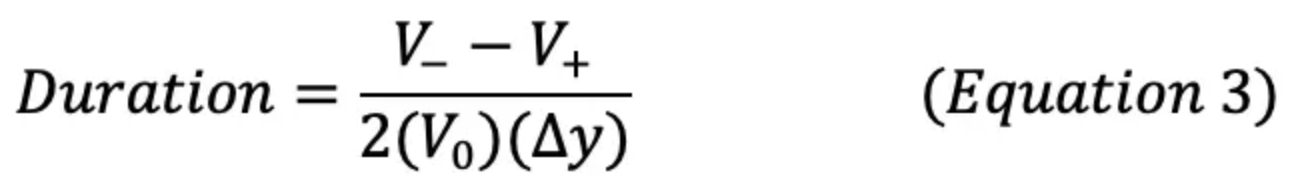
Where:
- V- is price of bond if market required yield decreases x bps
- V+ is price of bond if market required yield increases z bps
- Vo is price of bond at current market yield
- ▵y is z bps (expressed as decimal)
A few things to take note of:
- V- and V+ are derived from equation two
- The above equation will provide a number, and the unit of measure is in years. This does not directly reference time, rather it means “x bond has a price sensitivity to rate changes which is the same as a ___ year zero coupon bond.”
From the above equation, the approximate percentage change in bond price (A) for any given change in rates can be calculated as follows:
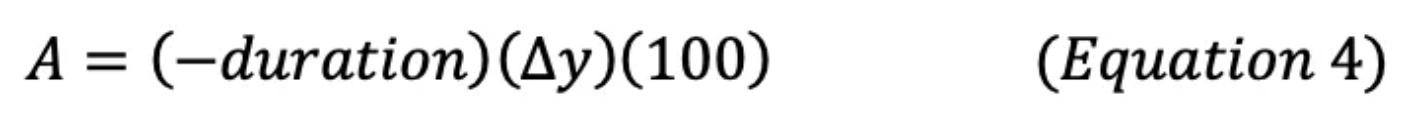
Where:
- ▵y is the change in market required yield, in bps (expressed as decimal)
This relationship can be applied to any change in basis points because the duration equation is a linear function. Remember the price/yield curve from earlier? Here it is again, with the addition of duration (dashed line).
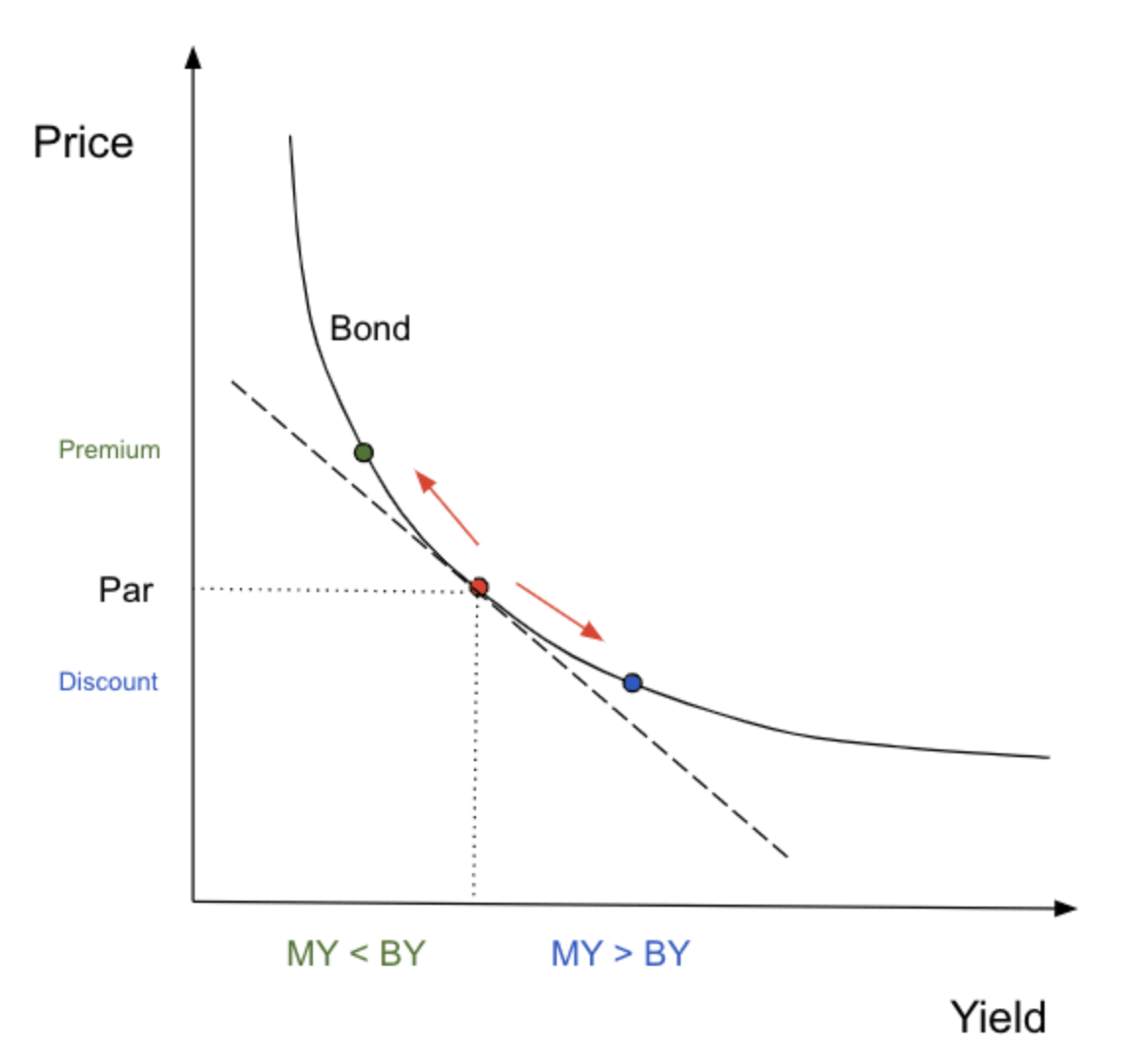
Notice two things: duration approximates the change in bond price much more accurately if the change in yield is small, and duration calculations will always underestimate price. Given the fact that duration is linear, while the price/yield curve is convex in shape, this should be evident.
So, since duration is not entirely accurate, how can we improve upon it?
CONVEXITY: THE SECOND DERIVATIVE
It is actually only a coincidence that the second derivative is termed convexity, while the shortcoming of the duration calculation is that it fails to account for the convexity of the price/yield curve. Regardless, it is useful to help us remember the concept…
In other words, convexity helps to measure the change in bond price as a function of the change in yield that is not explained by duration.
A picture here is helpful:
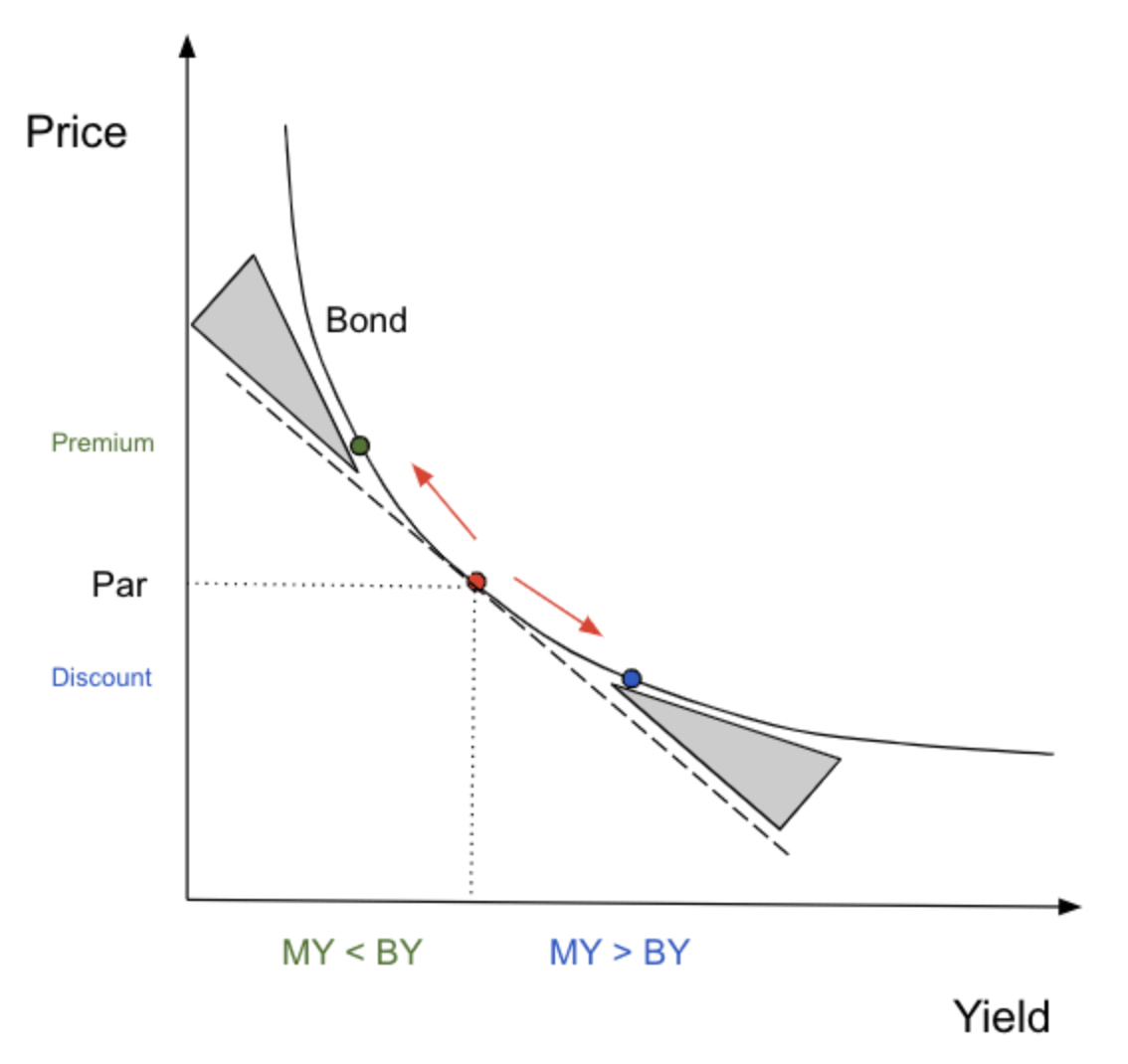
Convexity, as is shown, “adjusts” the duration estimate by the amount in the shaded gray area. This “convexity measure,” C, can be calculated as follows:
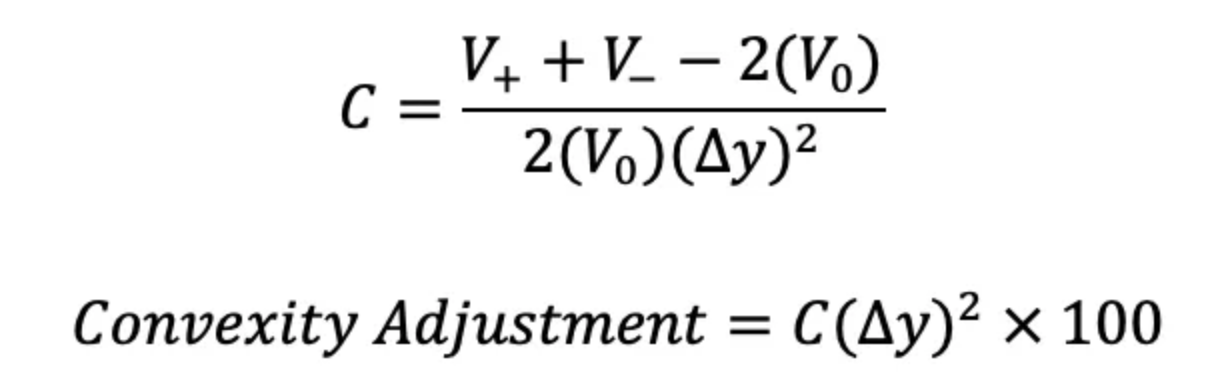
Armed with this knowledge, you are now able to calculate the approximate price change of a bond as a function of the changes in market required yield/interest rates. I would emphasize that performing the actual calculations isn’t necessary, but understanding the concepts is. For example, it should now make sense that for a 100 bps increase in market yield, the price of long-dated (30-year) bonds will drop approximately 20%. All that said, I’m still not sure what a Taylor series is (so don’t ask).
CONCLUSION
You now (hopefully) have a better understanding of the credit markets, bonds and bond math. In the next installment (part two), we will build on this knowledge by diving into bond risks and contagion.
In closing, we emphatically reiterate: Choose your store of value wisely. Never stop learning. The world is dynamic.